EE982
-ELETROMAGNETISMO AVANÇADO
AULA 10 2013.01 PPGEE-UFPE
PROBLEMAS DE VALORES DE FRONTEIRA II
10.1
Equação de Laplace
em Esféricas
Considera
Em esféricas
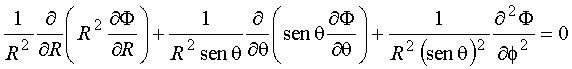
ou equivalentemente
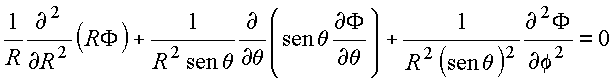
Assume
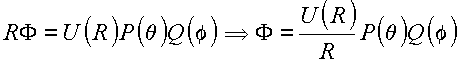
vem
Copyrigth 1999-2013 by Eduardo Fontana
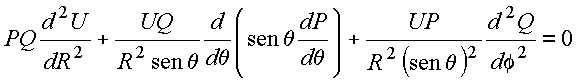
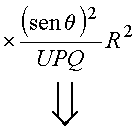
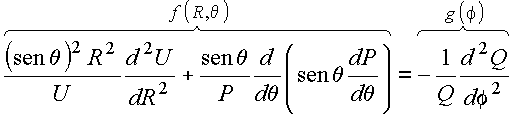
Pelos argumentos utilizados anteriormente, ambos os termos são constantes. Seja:
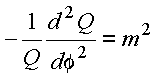
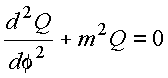
Considerando problemas envolvendo toda a variação azimutal, tem-se
Copyrigth 1999-2013 by Eduardo Fontana
Considere
a equação nas coordenadas 
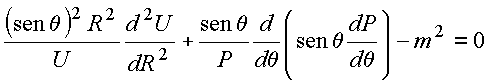
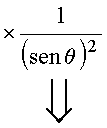
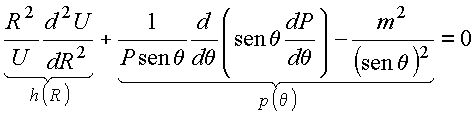
Para a constante de separação seja a escolha
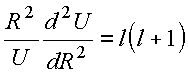
Obtém:
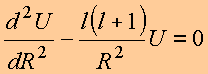(1)
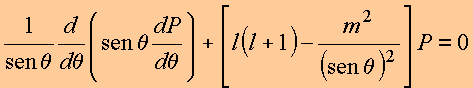(2)
Copyrigth 1999-2013 by Eduardo Fontana
Solução
de (1): Usa método de Frobenius, com apenas uma potência
de 
, i.e., seja
com 
a ser
determinado.
Insere em (1), vem
que tem como soluções
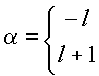
Assim
e dependência radial da função potencial é da forma
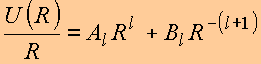
Solução de (2):
Define 
, com 
. Tem-se
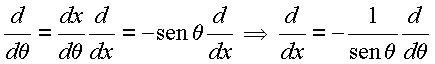
Insere essas transformações em (2), vem
Copyrigth 1999-2013 by Eduardo Fontana
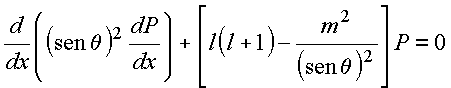
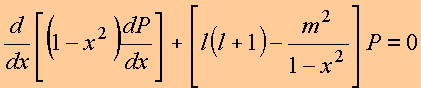(3)
A Eq.(3)
é a Equação de Legendre Generalizada.
10.2
Polinômios de
Legendre
Caso
1, m =0. Na ausência de
variação com a coordenada 
, a Eq.(3) fica reduzida para a Equação de
Legendre
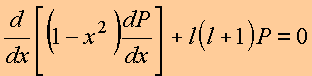(4)
A solução de (4) é obtida pelo Método de Frobenius. Assume
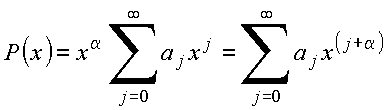(5)
Tem-se
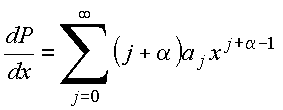
Copyrigth 1999-2013 by Eduardo Fontana
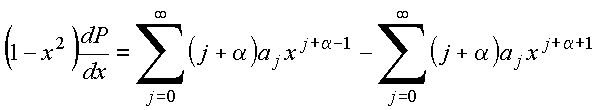
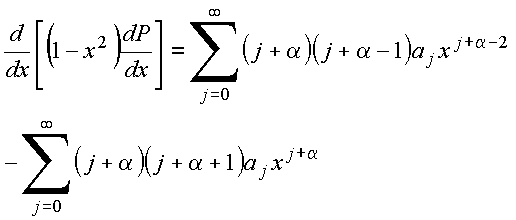(6)
Inserindo (5) e (6) em (4), vem
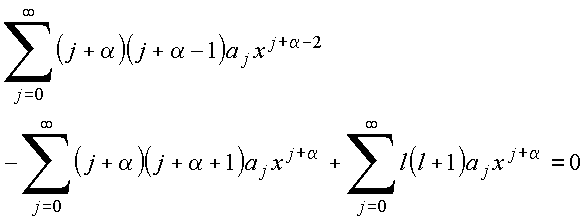
Essa combinação pode ser re-arranjada na forma
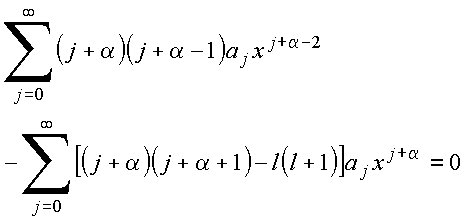
Copyrigth 1999-2013 by Eduardo Fontana
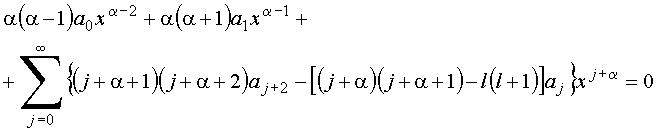Para que essa expansão seja nula 
deve-se
impor
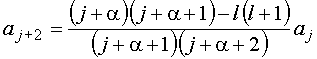(i)
(ii)
(iii)
Observações:
·
não
podem ser
nulos simultaneamente devido à condição (iii).
·
podem
ser
simultaneamente não nulos,
mas a
seqüência de coeficientes gerados por 
são
independentes. A
série de potências é soma de termos pares e ímpares. Os
coeficientes dos termos
pares são independentes dos coeficientes dos termos ímpares.
Essa seria
portanto uma soma de duas soluções.
·
Soluções independentes são obtidas
com 
ou com 
, como verificado abaixo.
Copyrigth 1999-2013 by Eduardo Fontana
Caso 1: 
. (ii) é
satisfeita.
(i) é satisfeita se
Caso 2: 
. (i) é
satisfeita.
(ii) é satisfeita se
Isso mostra que os casos 1 e 2 são equivalentes. Basta escolher uma das duas situações apenas. Seja a escolha
Tem-se:
(função par)
(função Ímpar)
Pode-se mostrar que:
·
Solução converge 
·
Série diverge para
a menos
que tenha um
número finito de termos. De
fato, para 
a relação
de
recorrência se torna
Copyrigth 1999-2013 by Eduardo Fontana
e a soma
diverge se 
. Para
evitar que a
série divirja, é necessário que haja um número finito de termos,
o que implica
que o parâmetro l seja inteiro.
Se 
e 
tem-se
Caso 1: 
e a série é da forma
com l par (pois J é par)
Caso 2: 
e a série é da forma
com l ímpar (pois J é par)
Copyrigth 1999-2013 by Eduardo Fontana
Exemplos:
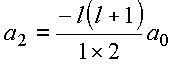
O
coeficiente 
do
polinômio de
Legendre é escolhido tal que 
. No caso acima, 
e
portanto
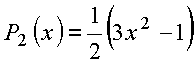
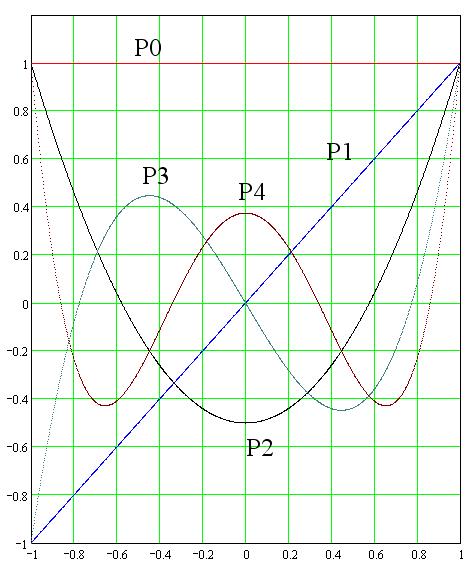
Polinômios de mais baixa ordem
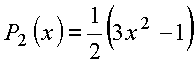
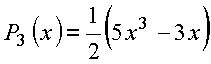
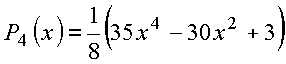
Copyrigth 1999-2013 by Eduardo Fontana
|
Em Mathcad a sintaxe dos polinômios de Legendre é: |
Copyrigth 1999-2013 by Eduardo Fontana
10.3 Propriedades dos polinômios de Legendre
1. Fórmula de Rodrigues
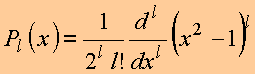
2. Ortogonalidade
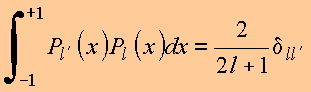
3.
Expansão de funções no domínio 
Definindo o produto escalar de funções reais no domínio
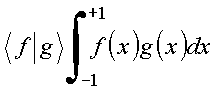
Tem-se
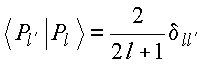
Como os polinômios de Legendre são funções ortogonais então para f uma função arbitrária nesse domínio
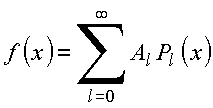
Copyrigth 1999-2013 by Eduardo Fontana
com
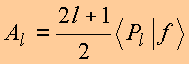
4. Completeza
Das relações anteriores,
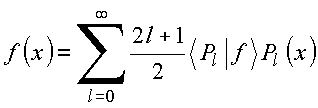
ou equivalentemente
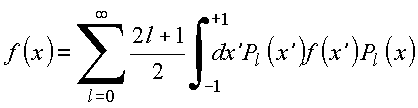
que pode ser posto na forma
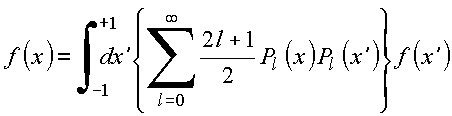
Essa última relação permite identificar a relação de completeza
Copyrigth 1999-2013 by Eduardo Fontana
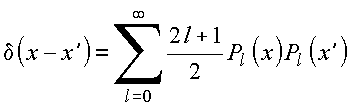
5. Algumas relações de recorrência
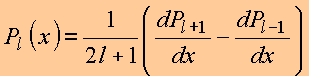
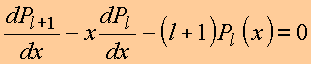
6. Valores específicos
]
, l ímpar
Copyrigth 1999-2013 by Eduardo Fontana