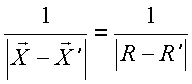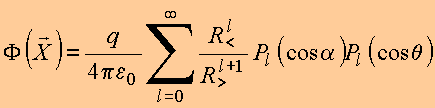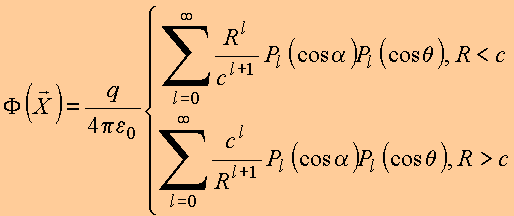EE982
-ELETROMAGNETISMO AVANÇADO
AULA 12 2013.01 PPGEE-UFPE
12.1 EXPANSÃO DA FUNÇÃO INVERSA
Uma função que surge
freqüentemente em expressões de campo é a função inversa.
Ex1. Potencial de uma distribuição de cargas
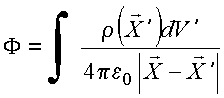
Ex.2. Função de Green
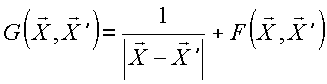
com ![]() , etc.
, etc.
A função inversa pode ser expandida em diferentes funções de base. Considera por exemplo a expansão em polinômios de Legendre. Com base na figura seguinte
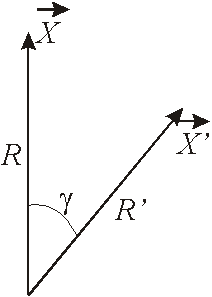
Copyrigth 1999-2013 by Eduardo Fontana
Para![]() :
:
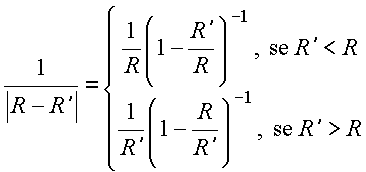
ou equivalentemente,
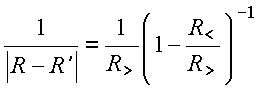
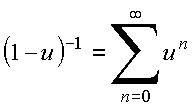
obtém
Copyrigth 1999-2013 by Eduardo Fontana
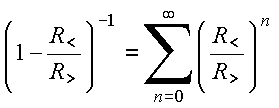
Portanto,
se ![]()
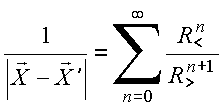
Note-se que:
·
A função 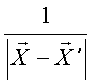 só
depende de
só
depende de ![]()
·
A expressão obtida para ![]() pode ser
generalizada
cf Aula 11, incluindo em cada termo da série o polinômio de
Legendre no índice
correspondente, ou seja, para
pode ser
generalizada
cf Aula 11, incluindo em cada termo da série o polinômio de
Legendre no índice
correspondente, ou seja, para ![]() quaisquer:
quaisquer:
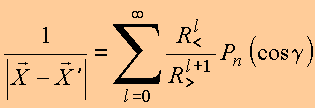
que representa, assim, a expansão da função inversa em polinômios de Legendre.
Copyrigth 1999-2013 by Eduardo Fontana
Exemplo: Potencial da espira carregada.
Para a determinação da função potencial da espira de carga uniformemente distribuída mostrada na figura
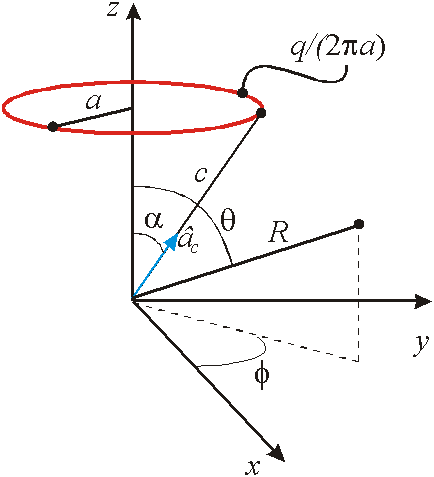
No eixo z:
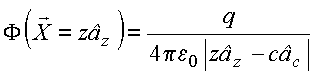
Usa expansão da função inversa, obtém:
Copyrigth 1999-2013 by Eduardo Fontana
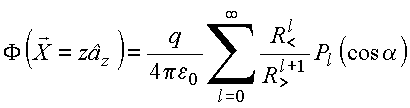
com ![]() representando
o
menor(maior) entre z e c.
Esse é o resultado no eixo z.
Conforme aula anterior, o resultado é generalizado
fazendo-se:
representando
o
menor(maior) entre z e c.
Esse é o resultado no eixo z.
Conforme aula anterior, o resultado é generalizado
fazendo-se:
Copyrigth 1999-2013 by Eduardo Fontana
Exemplo: Se a espira está no plano z=0:
![]() ,
, ![]()
obtém
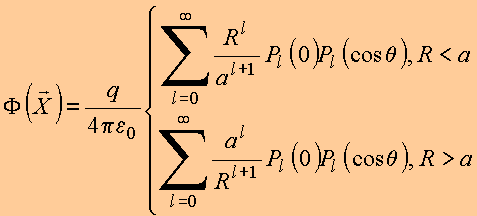
Da aula anterior:
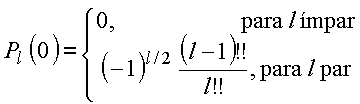
ou ainda,
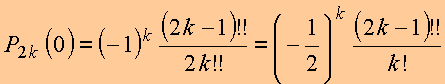
logo, no plano z = 0, tem-se:
Copyrigth 1999-2013 by Eduardo Fontana
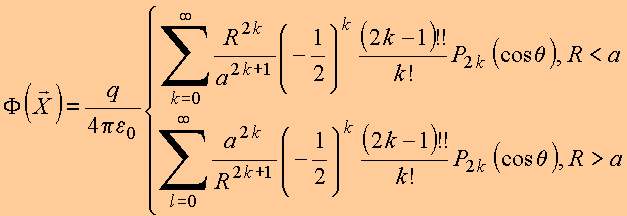
12.2 POLINÔMIOS ASSOCIADOS DE LEGENDRE
Considera
agora a situação em que ![]() que
fornece a equação
de Legendre generalizada na porção angular da função potencial.
que
fornece a equação
de Legendre generalizada na porção angular da função potencial.
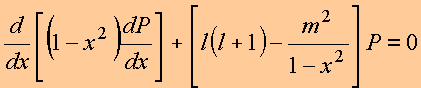
Características da solução:
i) l é inteiro
ii)
![]()
Copyrigth 1999-2013 by Eduardo Fontana
m >
0.
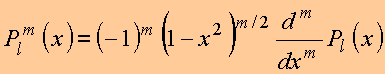
Utilizando a fórmula de Rodrigues para os polinômios de Legendre
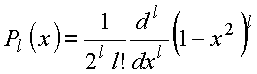
vem
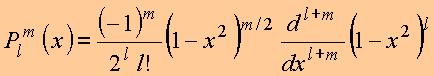
Alguns polinômios associados de Legendre (para m>0):
![]()
![]()
![]()
![]()
![]()
Expressões explícitas desses polinômios até a quarta ordem, além de outras informações, podem ser encontradas em
http://mathworld.wolfram.com/LegendrePolynomial.html
Copyrigth 1999-2013 by Eduardo Fontana
Propriedades
1.
Ortogonalidade no domínio![]()
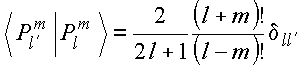
2.
Expansão de funções no domínio![]()
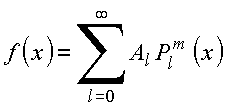
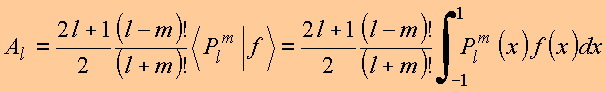
3. Completeza
Da Propriedade 2
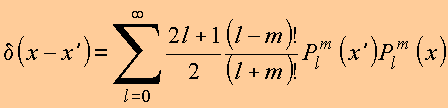
4. Polinômios associados para m < 0
Equação
generalizada depende de ![]() e
portanto
e
portanto ![]() . Para m
<
0 tem-se
. Para m
<
0 tem-se
Copyrigth 1999-2013 by Eduardo Fontana
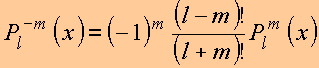
12.2 HARMÔNICOS ESFÉRICOS
Notando que
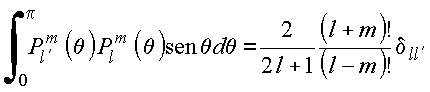
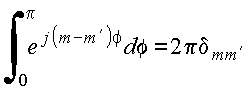
Define o harmônico esférico no par de índices (l,m) por:
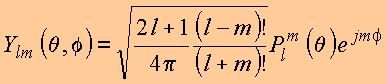
Com essa definição
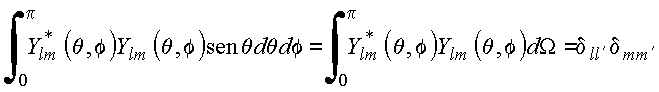 Ou equivalentemente, com o produto escalar definido no
domínio
Ou equivalentemente, com o produto escalar definido no
domínio ![]() , ou seja,
, ou seja,
Copyrigth 1999-2013 by Eduardo Fontana
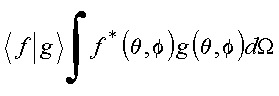
![]()
Expansão de funções
Harmônicos esféricos formam um conjunto completo no domínio de variação das variáveis angulares, ou seja:
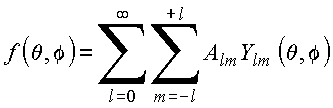

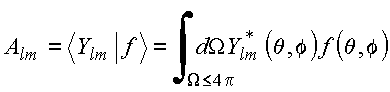
Completeza
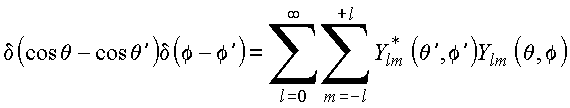
Copyrigth 1999-2013 by Eduardo Fontana
Simetria dos harmônicos esféricos
Dado que
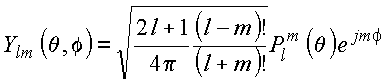

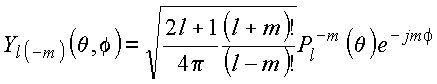
Por outro lado
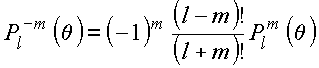
donde
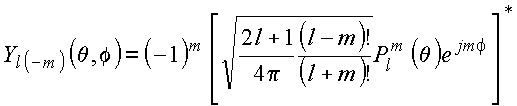

![]()
Copyrigth 1999-2013 by Eduardo Fontana
Alguns harmônicos esféricos
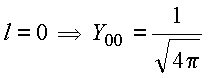
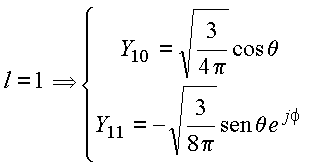
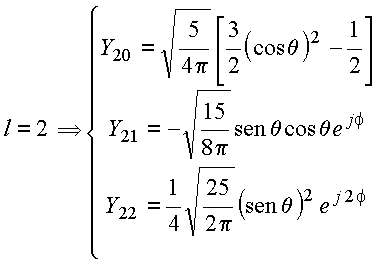
Observações
1.
![]()
2. Dado que
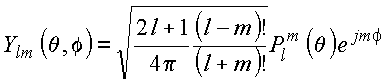
Copyrigth 1999-2013 by Eduardo Fontana
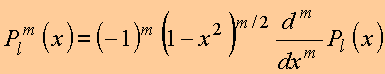
tem-se
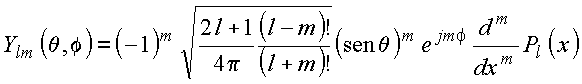
e portanto
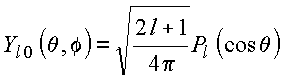
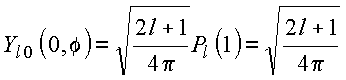
A
solução geral da equação de Laplace para ![]() é
portanto
é
portanto
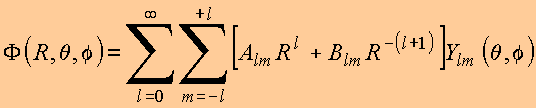
Propriedades adicionais dos harmônicos esféricos podem ser encontradas em
http://mathworld.wolfram.com/SphericalHarmonic.html
Copyrigth 1999-2013 by Eduardo Fontana