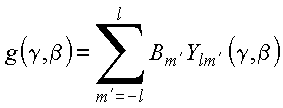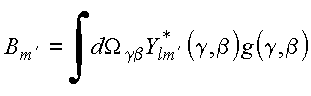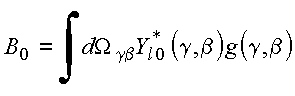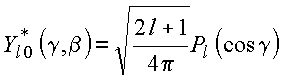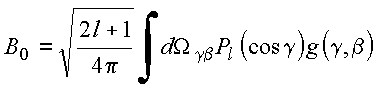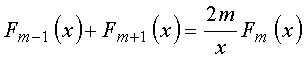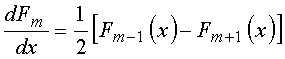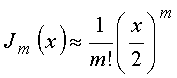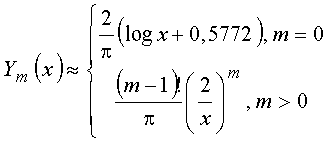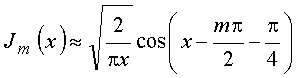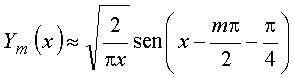EE982
-ELETROMAGNETISMO AVANÇADO
AULA 13 2013.01 PPGEE-UFPE
13.1
Teorema da Adição
para Harmônicos Esféricos
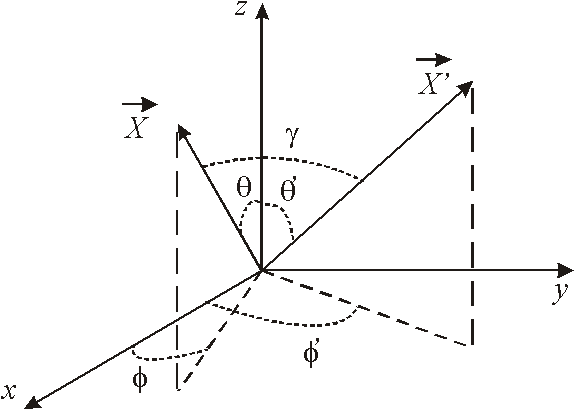
O teorema da adição para harmônicos esféricos representa uma importante expansão da função inversa. Pode ser sintetizado pela expressão
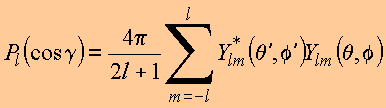
Copyrigth 1999-2013 by Eduardo Fontana
Demonstração:
Dado que
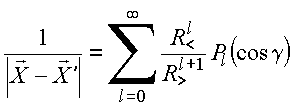 ,
,
e que
alternativamente, uma expansão em harmônicos esféricos pode ser
realizada, admitindo
fixo o vetor ![]() tem-se
tem-se
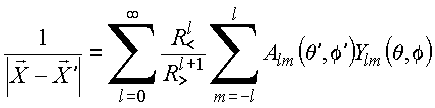
Nessa
expressão, cada coeficiente depende das variáveis angulares
associadas ao vetor
![]() .
.
A igualdade das duas expressões e ortogonalidade dos harmônicos esféricos fornece
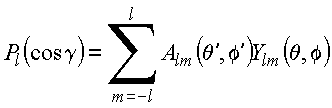
Utilizando a propriedade de ortogonalidade dos harmônicos esféricos, tem-se
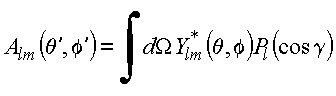
Copyrigth 1999-2013 by Eduardo Fontana
Note-se que a integral acima pode ser realizada em termos das variáveis angulares relativas mostradas na figura
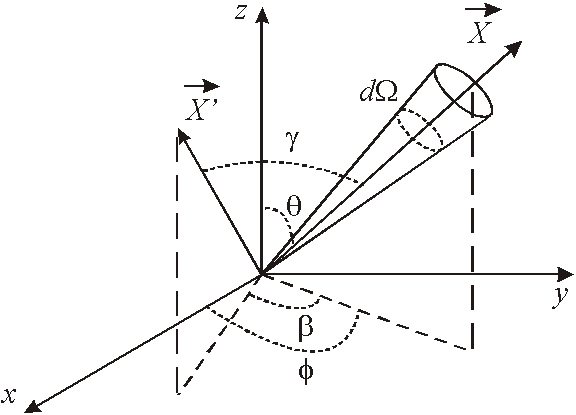
Fazendo-se a mudança de variáveis,
![]()
![]()
![]()
![]()
e com essa mudança de variáveis
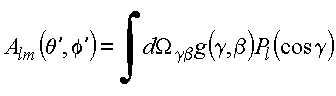
Copyrigth 1999-2013 by Eduardo Fontana
Copyrigth 1999-2013 by Eduardo Fontana
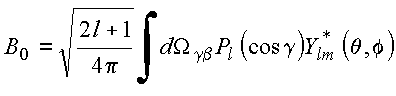
Utilizando
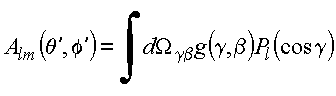
vem
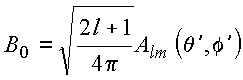
Para
obter o resultado final resta determinar o primeiro membro da
expressão
anterior. Note-se que a expansão da função ![]() para
para ![]() é
é
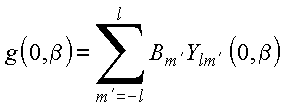
Dado que
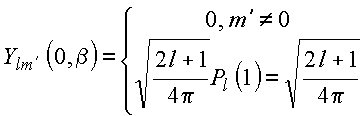
vem
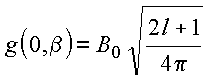
Copyrigth 1999-2013 by Eduardo Fontana
portanto,
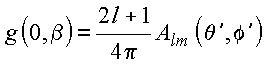
ou ainda
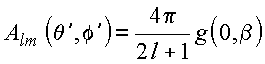
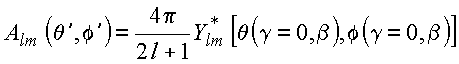
Note-se
que para ![]() ,
, ![]()
![]()
![]() ,
, ![]() , e portanto
, e portanto
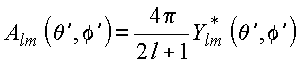
e finalmente utilizando
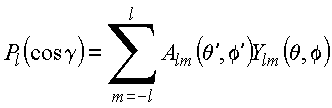
vem
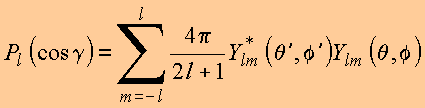
ou equivalentemente
Copyrigth 1999-2013 by Eduardo Fontana
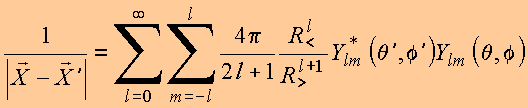
13.2
Solução geral da
Equação de Laplace em Cilíndricas
Em coordenadas cilíndricas
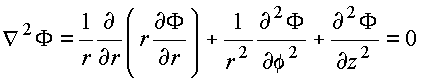
Assumindo
![]()
obtém
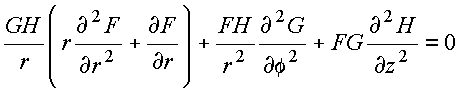
![]()
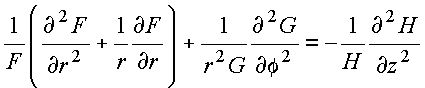
Conforme argumentado anteriormente, o resultado acima só pode ocorrer se
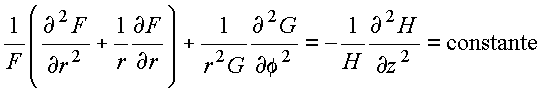
Copyrigth 1999-2013 by Eduardo Fontana
Seja a escolha da constante de separação
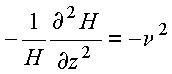
obtém
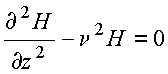
Solução geral
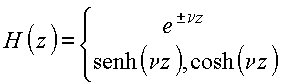
O restante da eq. diferencial se torna
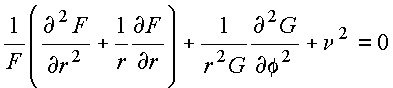
![]()
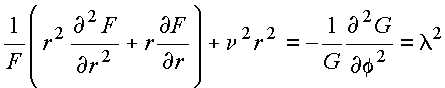
Obtém-se portanto duas equações diferenciais
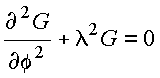 (I)
(I)
Copyrigth 1999-2013 by Eduardo Fontana
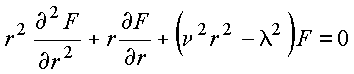
ou equivalentemente
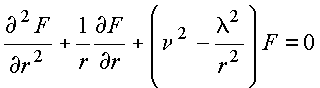 (II)
(II)
A solução de (I) é da forma
![]()
e para problemas
envolvendo toda a variação azimutal ![]()
Para a equação (II), seja
![]()
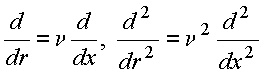
o que fornece
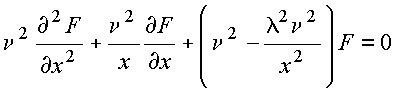
ou alternativamente
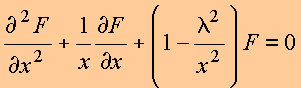 (III)
(III)
Copyrigth 1999-2013 by Eduardo Fontana
Para resolver (III), seja
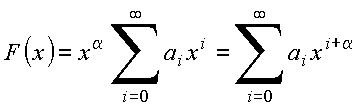
Inserindo em (III) vem
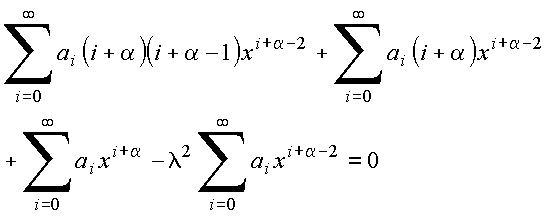
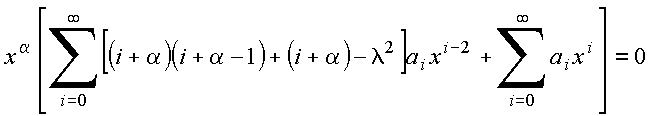
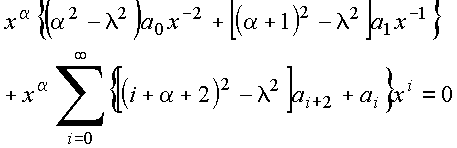
Para que
o primeiro membro seja nulo ![]() é
necessário que
é
necessário que
![]() (i)
(i)
Copyrigth 1999-2013 by Eduardo Fontana
![]() (ii)
(ii)
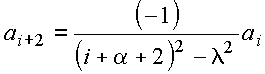 (iii)
(iii)
De (i): ![]()
![]()
De (ii):
![]()
![]()
Assim, se (i) for satisfeita, (ii) não pode ser satisfeita, e vice-versa, logo,
![]() ou
ou ![]()
Ambas as situações fornecem séries equivalentes como solução, i.e.:
|
|
|
|
Seja
portanto a escolha ![]() e
inicialmente
consideremos o caso
e
inicialmente
consideremos o caso ![]() . Tem-se
. Tem-se
Copyrigth 1999-2013 by Eduardo Fontana
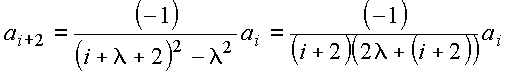
Seja ![]()
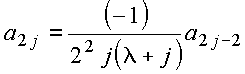
Obtém
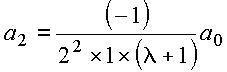
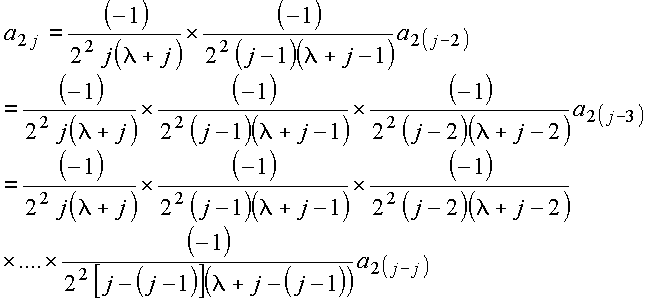
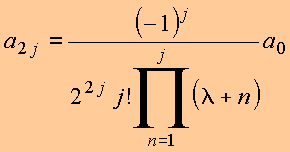
Copyrigth 1999-2013 by Eduardo Fontana
Para ![]() , note-se
que
, note-se
que
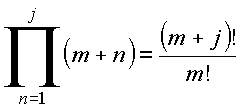
e portanto
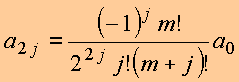
A
expressão geral para ![]() qualquer
pode ser
escrita em termos da função
qualquer
pode ser
escrita em termos da função ![]() , definida por
, definida por
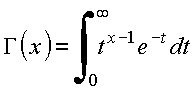
i) Para
argumento inteiro: ![]()
ii) Para
argumento arbitrário: ![]()
Com essas propriedades, tem-se
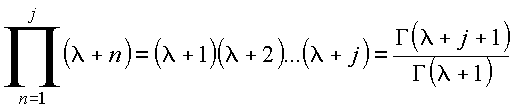
o que fornece
Copyrigth 1999-2013 by Eduardo Fontana
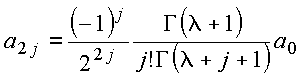
A solução pode ser escrita na forma
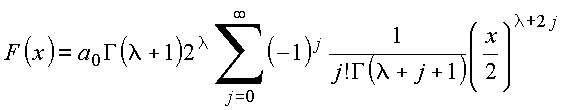
Geralmente escolhe-se
![]()
e a
série gerada é a função de Bessel do primeiro tipo de
ordem ![]()
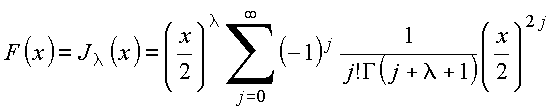
Para ![]() (inteiro), essa expressão reduz-se para
(inteiro), essa expressão reduz-se para
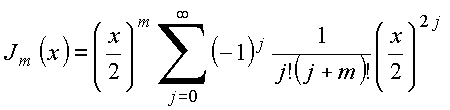
Copyrigth 1999-2013 by Eduardo Fontana
A
segunda solução, para ![]() não
inteiro, é obtida
fazendo-se
não
inteiro, é obtida
fazendo-se ![]() na
expressão
anterior, resultando em
na
expressão
anterior, resultando em
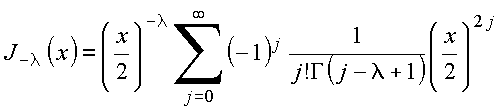
Essa
solução é linearmente independente da primeira para ![]() não
inteiro. Se
não
inteiro. Se ![]() a relação
de
recorrência (iii) é escrita na forma
a relação
de
recorrência (iii) é escrita na forma
![]()
Essa
relação mostra que para ![]()
![]()
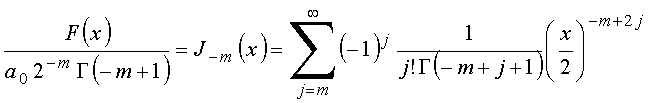 Na expressão acima,
fazendo
Na expressão acima,
fazendo
![]() com
com ![]() vem
vem
Copyrigth 1999-2013 by Eduardo Fontana
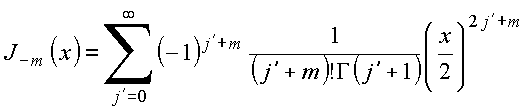
ou ainda
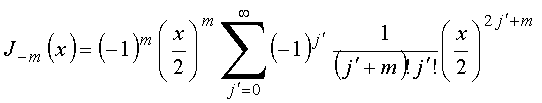
que fornece
E portanto, para valores inteiros, as duas soluções não são independentes.
Para contornar essa dificuldade, define-se a função de Neumann, também denominada de função de Bessel do segundo tipo
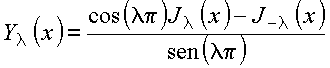
Para ![]() real esta
função é
independente da função de Bessel. Pode-se mostrar que no limite
real esta
função é
independente da função de Bessel. Pode-se mostrar que no limite
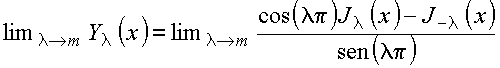
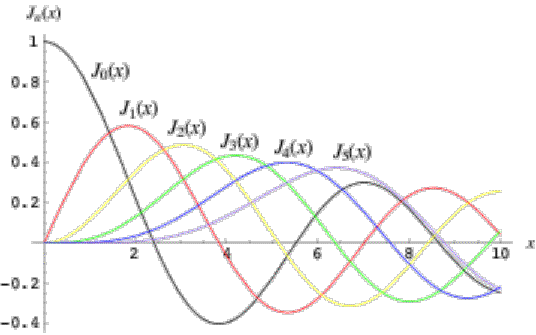
a função de Neumann também é independente da função de Bessel. Nas figuras seguintes estão ilustrados gráficos das funções de Bessel e de Neumann
(obtidos de http://mathworld.wolfram.com)
Copyrigth 1999-2013 by Eduardo Fontana
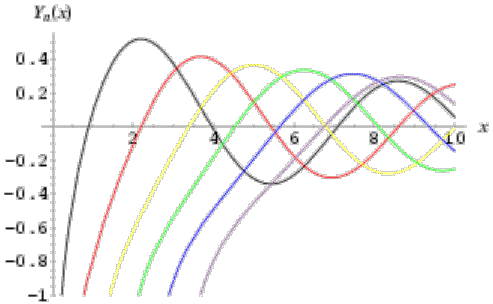
Copyrigth 1999-2013 by Eduardo Fontana
Observações:
i. As funções de Bessel do primeiro tipo não divergem, e as de segundo tipo divergem na origem
ii. Ambas as funções exibem comportamento oscilatório, e têm número infinito de raízes
iii. Em Mathcad, utiliza-se a sintaxe
Função
de Bessel do primeiro tipo, ordem zero: ![]()
Função
de Bessel do primeiro tipo, ordem um: ![]()
Função
de Bessel do primeiro tipo, ordem n: ![]()
Função
de Bessel do segundo tipo, ordem zero: ![]()
Função
de Bessel do segundo tipo, ordem um: ![]()
Função
de Bessel do segundo tipo, ordem n: ![]()
iv. As raízes das funções de Bessel podem ser obtidas numericamente. Alguns valores estão listados na tabela seguinte
|
|
k-ésima raiz de |
||
|
|
k=1 |
k=2 |
k=3 |
|
m=0 |
2,405 |
5,520 |
8,654 |
|
m=1 |
0 |
3,832 |
7,016 |
|
m=2 |
0 |
5,136 |
8,417 |
|
m=3 |
0 |
6,380 |
9,761 |
Copyrigth 1999-2013 by Eduardo Fontana
|
|
k-ésima raiz de |
||
|
|
k=1 |
k=2 |
k=3 |
|
m=0 |
0,894 |
3,958 |
7,086 |
|
m=1 |
2,197 |
5,430 |
8,596 |
Propriedades
(![]() :)
:)
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
Copyrigth 1999-2013 by Eduardo Fontana
|
5. |
|
|
6. |
Funções de Hankel (Funções de Bessel do terceiro tipo. Primeiro tipo: Segundo tipo: Definições em analogia com as definições de exponenciais complexas |
Copyrigth 1999-2013 by Eduardo Fontana