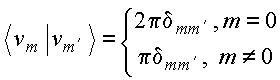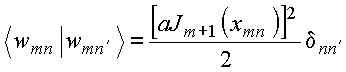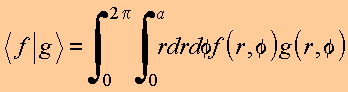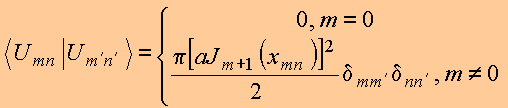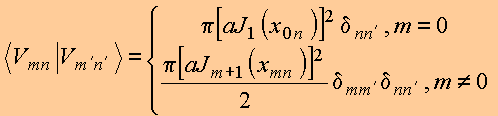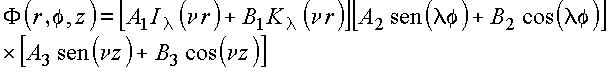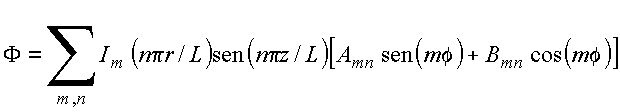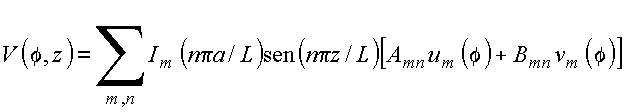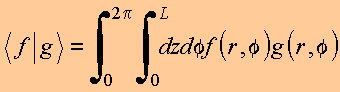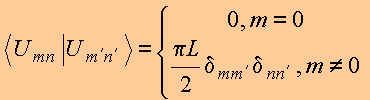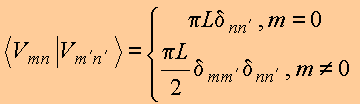EE982
-ELETROMAGNETISMO AVANÇADO
AULA 14 2013.01 PPGEE-UFPE
14.1
ORTOGONALIDADE DAS
FUNÇÕES DE BESSEL
Seja ![]() a n-ésima
raiz
de
a n-ésima
raiz
de ![]() , i.e.,
, i.e.,
![]()
Constrói-se o conjunto de funções
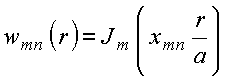
com a propriedade,
![]()
Note-se que
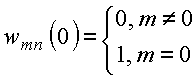
Define o
produto escalar, para funções reais, no espaço da variável
radial, no domínio ![]() , na forma
, na forma
Copyrigth 1999-2013 by Eduardo Fontana
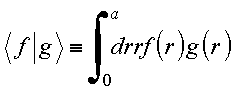
Pode-se mostrar que
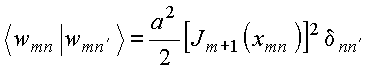
ou seja,
as funções ![]() são
ortogonais no
domínio
são
ortogonais no
domínio ![]() . Assim,
uma função
arbitrária
. Assim,
uma função
arbitrária ![]() pode ser
decomposta
na forma
pode ser
decomposta
na forma
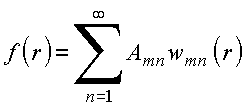
Note-se que cada índice m fornece um conjunto específico de coeficientes de expansão, obtidos da condição de ortogonalidade. Com o emprego dessa condição, aplicando o produto escalar em ambos os membros da expressão anterior, obtém-se
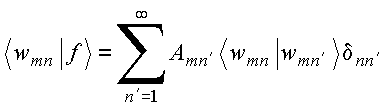
o que fornece
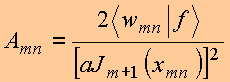
Copyrigth 1999-2013 by Eduardo Fontana
Em resumo, em coordenadas cilíndricas, foi gerada uma classe de soluções para a equação de Laplace da forma
![]()
com
![]()
![]()
![]()
com os
parâmetros ![]() a serem
determinados
para o PVF específico.
a serem
determinados
para o PVF específico.
14.2 FUNÇÕES DE BESSEL MODIFICADAS
Na equação diferencial original, posta na forma
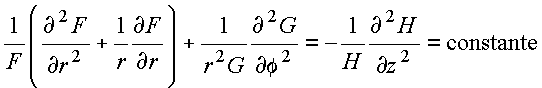
se a constante de separação fosse modificada de acordo com
![]()
Copyrigth 1999-2013 by Eduardo Fontana
Obteríamos
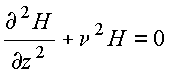
com solução geral do tipo
![]()
Uma vez
que a dependência em ![]() independe dessa constante de separação, a solução
geral nessa
variável permanece na forma
independe dessa constante de separação, a solução
geral nessa
variável permanece na forma
![]()
A solução da equação radial pode ser obtida fazendo-se a modificação
![]()
ou equivalentemente
![]()
e a solução geral da equação radial seria da forma
![]()
Copyrigth 1999-2013 by Eduardo Fontana
Para evitar o manuseio de funções complexas em problemas em que as soluções obtidas são funções puramente reais, definem-se:
Função
modificada de Bessel de 1a. espécie:
![]()
Função
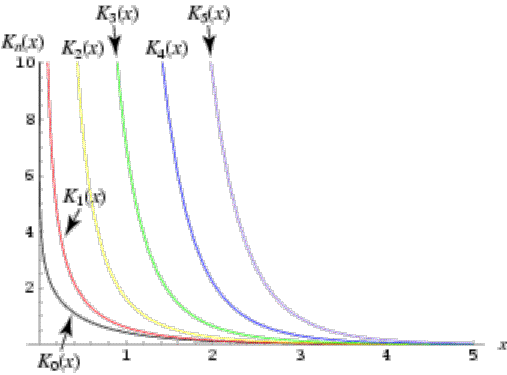
modificada de Bessel de 2a. espécie:
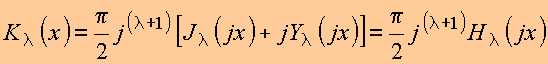
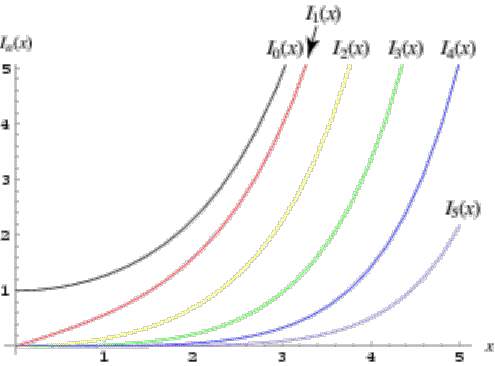
As figuras seguintes mostram as curvas correspondentes (obtidas de http://mathworld.wolfram.com)
Copyrigth 1999-2013 by Eduardo Fontana
Funções
modificadas de Bessel de 1a. espécie
Funções
modificadas de Bessel de 2a. espécie
Copyrigth 1999-2013 by Eduardo Fontana
![]()
![]()
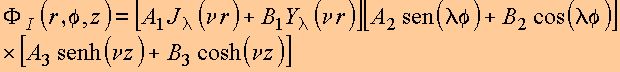
Copyrigth 1999-2013 by Eduardo Fontana
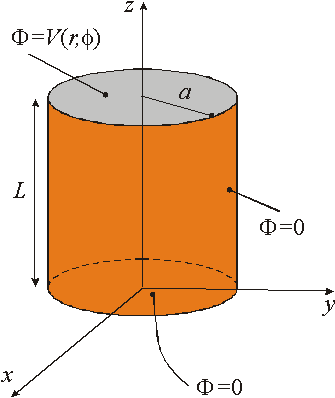
Copyrigth 1999-2013 by Eduardo Fontana
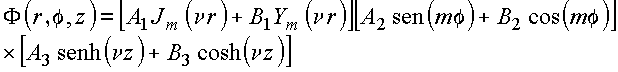
2. Uma vez que a solução é
finita no eixo z,
deve-se ter ![]() e a
solução pode ser
condensada na forma
e a
solução pode ser
condensada na forma
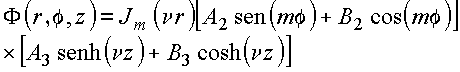
3. Como o potencial é nulo
em ![]() deve-se
ter
deve-se
ter ![]() , e a solução é reduzida para
, e a solução é reduzida para
![]()
4. Aplicando a condição de contorno na superfície lateral do cilindro, i.e.,
![]()
resulta em
![]()
e portanto
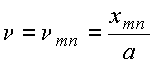
Copyrigth 1999-2013 by Eduardo Fontana
e obtém-se um conjunto infinito de soluções satisfazendo às condições de contorno na tampa inferior e superfície lateral, com forma geral
![]()
Copyrigth 1999-2013 by Eduardo Fontana
Copyrigth 1999-2013 by Eduardo Fontana
E portanto, os coeficientes da expansão podem ser calculados de
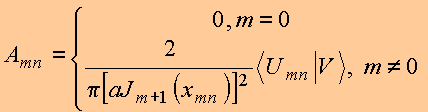
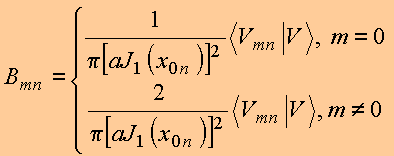
Copyrigth
1999-2013 by Eduardo Fontana
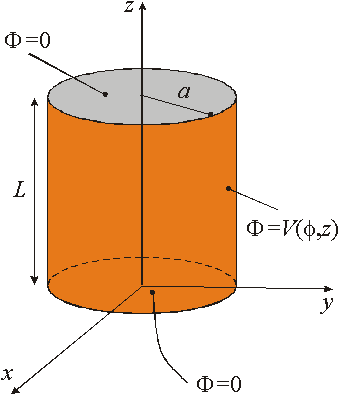
Copyrigth 1999-2013 by Eduardo Fontana
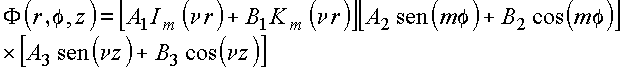
2. Uma vez que a solução é
finita no eixo z,
deve-se ter ![]() e a
solução pode ser
condensada na forma
e a
solução pode ser
condensada na forma
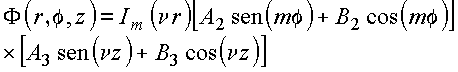
3. Como o potencial é nulo
em ![]() deve-se
ter
deve-se
ter ![]() , e a solução é reduzida para
, e a solução é reduzida para
![]()
4. Aplicando a condição de
contorno em ![]()
![]()
resulta em
![]()
e portanto
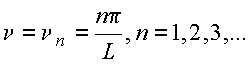
(note-se que ![]() é
excluído pois gera
como solução a solução trivial)
é
excluído pois gera
como solução a solução trivial)
Copyrigth 1999-2013 by Eduardo Fontana
Obtém-se um conjunto infinito de soluções satisfazendo às condições de contorno nas tampas superior e inferior
![]()
Copyrigth 1999-2013 by Eduardo Fontana
E portanto, os coeficientes da expansão podem ser calculados de
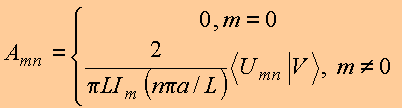
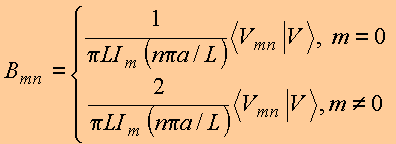
Copyrigth 1999-2013 by Eduardo Fontana
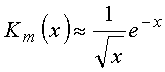
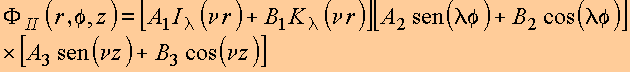
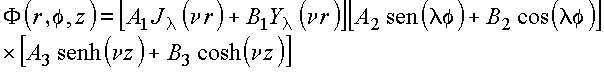
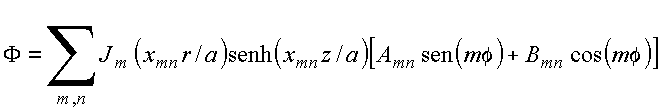
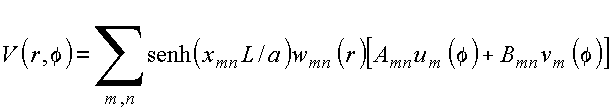 com
com